Exemplos De Diagonais De Um Polígono é um conceito fundamental na geometria, explorando as relações entre os lados e os vértices de figuras geométricas fechadas. As diagonais, linhas que conectam vértices não adjacentes, desempenham um papel crucial na compreensão da estrutura e propriedades dos polígonos.
Neste estudo, examinaremos a construção de diagonais em diversos polígonos, desde o triângulo até o hexágono, analisando a influência do número de lados na quantidade de diagonais e como as diagonais se comportam em polígonos convexos e côncavos. Abordaremos também as propriedades das diagonais em polígonos regulares, sua relação com os ângulos internos e como elas podem ser utilizadas para dividir polígonos em triângulos.
Conceitos Básásicos: Exemplos De Diagonais De Um Polígono
Uma diagonal de um polígono é um segmento de reta que conecta dois vértices não adjacentes do polígono. Em outras palavras, uma diagonal é uma linha que atravessa o interior do polígono, conectando dois pontos da sua borda sem passar por nenhum outro ponto da borda.
Número de Diagonais
O número de diagonais que um polígono possui pode ser calculado utilizando a seguinte fórmula:
D = n(n-3)/2
Onde:* D é o número de diagonais
n é o número de lados do polígono
Comparação entre Diagonais e Lados
O número de diagonais em um polígono está diretamente relacionado ao número de lados. À medida que o número de lados aumenta, o número de diagonais também aumenta. No entanto, o número de diagonais cresce a um ritmo mais rápido do que o número de lados.Por exemplo, um triângulo (3 lados) não possui diagonais, um quadrado (4 lados) possui 2 diagonais, um pentágono (5 lados) possui 5 diagonais, e um hexágono (6 lados) possui 9 diagonais.
Exemplos de Diagonais em Polígonos
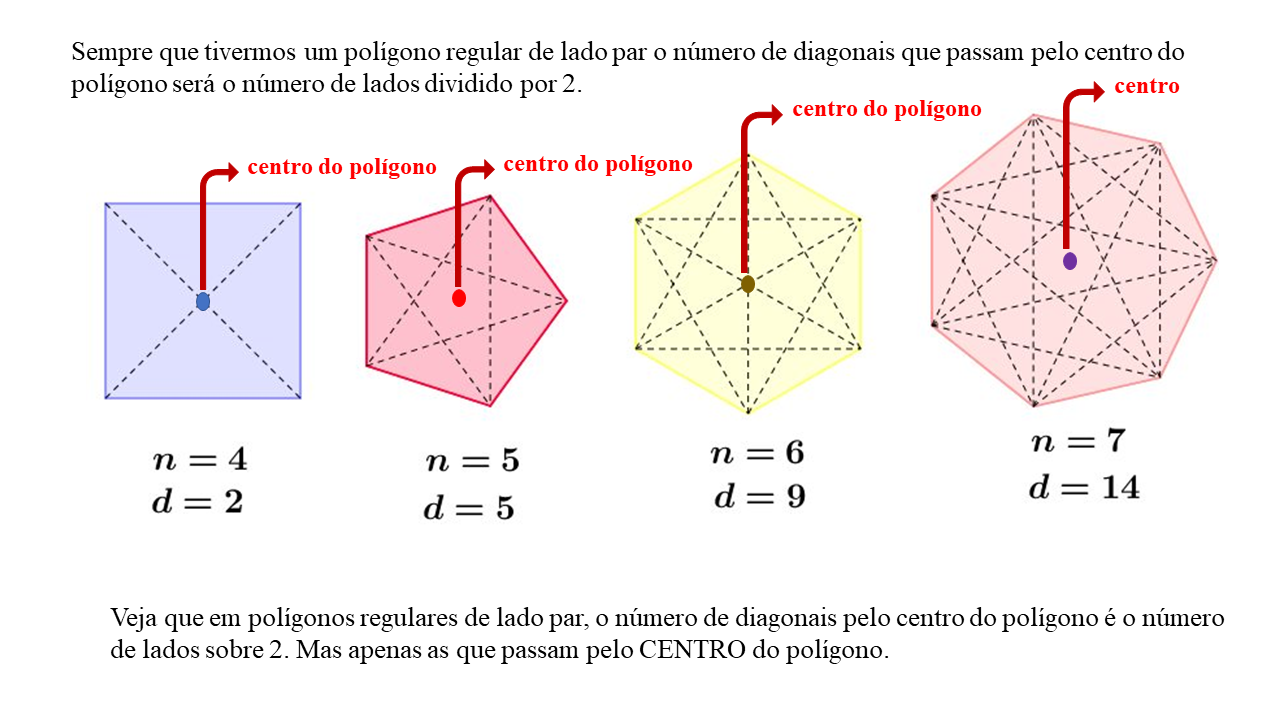
As diagonais de um polígono são segmentos de reta que ligam dois vértices não adjacentes. Para compreender melhor o conceito de diagonais, vamos analisar alguns exemplos.
Exemplos de Diagonais em Diferentes Polígonos
A tabela a seguir apresenta exemplos de diagonais em diferentes polígonos, mostrando o número de lados, o número de diagonais e exemplos de diagonais com desenhos.
| Nome do Polígono | Número de Lados | Número de Diagonais | Exemplos de Diagonais |
|---|---|---|---|
| Triângulo | 3 | 0 |
Um triângulo não possui diagonais, pois todos os seus vértices são adjacentes. |
| Quadrado | 4 | 2 |
Um quadrado possui duas diagonais, que se cruzam no centro do quadrado. As diagonais dividem o quadrado em quatro triângulos isósceles congruentes. |
| Pentágono | 5 | 5 |
Um pentágono possui cinco diagonais. Cada vértice pode ser ligado a dois vértices não adjacentes, resultando em cinco diagonais. |
| Hexágono | 6 | 9 |
Um hexágono possui nove diagonais. Cada vértice pode ser ligado a três vértices não adjacentes, resultando em nove diagonais. |
Construção de Diagonais em Polígonos
A construção de diagonais em um polígono é simples: basta ligar dois vértices não adjacentes do polígono por um segmento de reta.
Por exemplo, para construir uma diagonal em um triângulo, podemos escolher dois vértices quaisquer e traçar uma linha reta entre eles. Como todos os vértices de um triângulo são adjacentes, não é possível traçar nenhuma diagonal.
No caso do quadrado, podemos traçar duas diagonais: uma ligando os vértices opostos e outra ligando os vértices adjacentes. As diagonais do quadrado se cruzam no centro do quadrado.
Para um pentágono, podemos traçar cinco diagonais, conectando cada vértice a dois vértices não adjacentes.
No hexágono, podemos traçar nove diagonais, conectando cada vértice a três vértices não adjacentes.
Comparação da Construção de Diagonais em Polígonos Convexos e Côncavos
A construção de diagonais em polígonos convexos e côncavos é similar, porém existem algumas diferenças importantes.
Em um polígono convexo, todas as diagonais estão totalmente contidas no interior do polígono. Isso significa que todas as diagonais estão dentro do polígono e não intersectam nenhum lado do polígono.
Em um polígono côncavo, algumas diagonais podem estar parcialmente ou totalmente fora do polígono. Isso ocorre porque alguns vértices do polígono côncavo estão “para dentro” do polígono, o que faz com que algumas diagonais cruzem os lados do polígono.
Em resumo, a construção de diagonais em polígonos convexos é mais simples, pois todas as diagonais estão dentro do polígono. Em polígonos côncavos, algumas diagonais podem estar fora do polígono, o que torna a construção mais complexa.
Propriedades das Diagonais

As diagonais de um polígono possuem características e relações importantes que influenciam sua geometria e propriedades. Ao analisarmos as diagonais de um polígono, podemos observar padrões e relações que nos permitem compreender melhor sua estrutura e comportamento.
Diagonais de Polígonos Regulares
As diagonais de um polígono regular possuem propriedades específicas que decorrem da simetria e regularidade do polígono.
- Todas as diagonais de um polígono regular têm o mesmo comprimento.
- As diagonais de um polígono regular dividem o polígono em triângulos isósceles congruentes.
- As diagonais de um polígono regular formam ângulos iguais com os lados do polígono.
Por exemplo, em um hexágono regular, todas as diagonais têm o mesmo comprimento e dividem o hexágono em seis triângulos equiláteros congruentes.
Relação entre Diagonais e Ângulos Internos
As diagonais de um polígono estão diretamente relacionadas com os ângulos internos do polígono.
- A soma dos ângulos internos de um polígono pode ser calculada utilizando o número de diagonais que podem ser traçadas a partir de um vértice.
- A relação entre o número de diagonais e o número de lados de um polígono é expressa pela fórmula:
n(n-3)/2
, onde ‘n’ é o número de lados do polígono.
Por exemplo, em um pentágono, podemos traçar duas diagonais a partir de um vértice, e a soma dos ângulos internos do pentágono é 540 graus.
Divisão de um Polígono em Triângulos
As diagonais de um polígono podem ser utilizadas para dividir o polígono em triângulos.
- O número de triângulos que um polígono pode ser dividido é igual ao número de lados menos dois.
- A divisão de um polígono em triângulos facilita o cálculo da área do polígono, pois a área de cada triângulo pode ser calculada separadamente.
Por exemplo, um hexágono pode ser dividido em quatro triângulos, e a área do hexágono pode ser calculada somando as áreas dos quatro triângulos.
Através da análise de exemplos concretos e da aplicação de conceitos matemáticos, compreendemos como as diagonais de um polígono são elementos importantes para a caracterização e análise de suas propriedades geométricas. A capacidade de calcular o número de diagonais e de identificar suas propriedades em diferentes tipos de polígonos fornece uma base sólida para o estudo da geometria plana.

