Exemplos De Coeficiente De Correlação De Pearson, essa ferramenta poderosa da estatística, nos permite desvendar a relação entre duas variáveis. Imagine que você quer saber se a quantidade de horas estudadas influencia a nota final em um exame. O coeficiente de correlação de Pearson nos dá uma medida numérica dessa relação, indicando se existe uma tendência de uma variável aumentar ou diminuir à medida que a outra muda, e qual a força dessa relação.
Utilizando essa medida, podemos identificar padrões em dados, fazer previsões e tomar decisões mais informadas. Seja na área da saúde, economia, finanças ou qualquer outra, o coeficiente de correlação de Pearson se torna um aliado fundamental na análise de dados e na busca por insights relevantes.
Introdução ao Coeficiente de Correlação de Pearson
Imagine que você está analisando dados sobre o número de horas que os alunos estudam e suas notas finais em uma determinada matéria. Você percebe que, geralmente, os alunos que estudam mais tendem a ter notas mais altas. Essa relação entre as variáveis “horas de estudo” e “notas” é o que chamamos de correlação.
A correlação é um conceito fundamental na análise de dados, pois nos permite entender como duas variáveis se relacionam. Essa relação pode ser positiva, negativaou nula. No exemplo das horas de estudo e notas, a correlação é positiva, pois à medida que uma variável aumenta, a outra também tende a aumentar.
O Coeficiente de Correlação de Pearson
O Coeficiente de Correlação de Pearson, também conhecido como coeficiente de correlação linear, é uma medida estatística que quantifica a força e a direção da relação linear entre duas variáveis. Ele varia de
-1 a +1, sendo que
* +1:Indica uma correlação linear perfeita e positiva. Isso significa que as duas variáveis variam juntas na mesma direção, com uma relação perfeitamente linear.
-1
Indica uma correlação linear perfeita e negativa. Isso significa que as duas variáveis variam juntas em direções opostas, com uma relação perfeitamente linear.
0
Indica ausência de correlação linear. Isso significa que não existe uma relação linear entre as variáveis.
Interpretação do Coeficiente de Correlação de Pearson, Exemplos De Coeficiente De Correlação De Pearson
O coeficiente de correlação de Pearson nos fornece informações importantes sobre a relação entre duas variáveis. * Correlação positiva:Indica que as duas variáveis tendem a variar juntas na mesma direção. Por exemplo, se o coeficiente de correlação entre a altura e o peso de uma pessoa for positivo, significa que pessoas mais altas tendem a ser mais pesadas.
Correlação negativa
Indica que as duas variáveis tendem a variar juntas em direções opostas. Por exemplo, se o coeficiente de correlação entre o número de horas trabalhadas e a qualidade do sono for negativo, significa que pessoas que trabalham mais horas tendem a ter menos qualidade de sono.
Correlação nula
Indica que não existe uma relação linear entre as variáveis. Por exemplo, se o coeficiente de correlação entre a altura de uma pessoa e a cor dos seus olhos for zero, significa que não existe uma relação linear entre essas duas variáveis.É importante lembrar que o coeficiente de correlação de Pearson apenas mede a relação linear entre duas variáveis.
Se a relação não for linear, o coeficiente de correlação pode não ser uma medida adequada.
Cálculo do Coeficiente de Correlação de Pearson
Agora que você já entendeu o que é o coeficiente de correlação de Pearson e como ele pode ser usado para medir a força da relação linear entre duas variáveis, vamos aprender como calculá-lo.
Fórmula do Coeficiente de Correlação de Pearson
A fórmula para calcular o coeficiente de correlação de Pearson é:
r = Σ[(Xi
- X̄)(Yi
- Ȳ)] / √[Σ(Xi
- X̄)²
- Σ(Yi
- Ȳ)²]
Onde:
- r é o coeficiente de correlação de Pearson
- Xi é o i-ésimo valor da variável X
- Yi é o i-ésimo valor da variável Y
- X̄ é a média da variável X
- Ȳ é a média da variável Y
- Σ é a soma de todos os valores
Exemplo Prático de Cálculo
Vamos usar um exemplo prático para ilustrar como calcular o coeficiente de correlação de Pearson. Imagine que você está estudando a relação entre o número de horas que os alunos estudam por semana e suas notas finais em um curso de matemática.
Você coletou dados de 5 alunos e os resultados estão na tabela abaixo:
| Aluno | Horas de Estudo (X) | Nota Final (Y) | (Xi
|
(Yi
|
(Xi
|
(Xi
|
(Yi
|
|---|---|---|---|---|---|---|---|
| 1 | 5 | 70 | -2 | -10 | 20 | 4 | 100 |
| 2 | 7 | 80 | 0 | 0 | 0 | 0 | 0 |
| 3 | 9 | 90 | 2 | 10 | 20 | 4 | 100 |
| 4 | 10 | 95 | 3 | 15 | 45 | 9 | 225 |
| 5 | 12 | 100 | 5 | 20 | 100 | 25 | 400 |
| Total | 33 | 435 | 185 | 42 | 825 |
Calculando as médias:
- X̄ = ΣXi / n = 33 / 5 = 6.6
- Ȳ = ΣYi / n = 435 / 5 = 87
Agora, podemos calcular o coeficiente de correlação de Pearson usando a fórmula:
r = Σ[(Xi
- X̄)(Yi
- Ȳ)] / √[Σ(Xi
- X̄)²
- Σ(Yi
- Ȳ)²] = 185 / √(42
- 825) = 0.96
O coeficiente de correlação de Pearson é 0.96, o que indica uma correlação positiva forte entre o número de horas que os alunos estudam e suas notas finais em matemática.
Aplicações do Coeficiente de Correlação de Pearson
O coeficiente de correlação de Pearson, como vimos, é uma ferramenta poderosa para quantificar a relação linear entre duas variáveis. Mas como essa medida se aplica ao mundo real? Nesta seção, vamos explorar algumas das aplicações do coeficiente de correlação em diferentes áreas.
Aplicações do Coeficiente de Correlação de Pearson em Diferentes Áreas
A aplicação do coeficiente de correlação de Pearson é ampla, abrangendo diversos campos de estudo, como saúde, economia e finanças. Vamos explorar alguns exemplos concretos:
- Na área da saúde, o coeficiente de correlação pode ser utilizado para analisar a relação entre o consumo de alimentos ricos em fibras e o risco de desenvolver doenças cardíacas. Por exemplo, um estudo poderia analisar a correlação entre a ingestão diária de fibras e a probabilidade de um indivíduo sofrer um ataque cardíaco.
Se o coeficiente de correlação for alto e positivo, isso significaria que um maior consumo de fibras está associado a um menor risco de doenças cardíacas.
- Na economia, o coeficiente de correlação pode ser usado para analisar a relação entre o crescimento econômico e o desemprego. Um estudo poderia analisar a correlação entre o PIB de um país e a taxa de desemprego. Se o coeficiente de correlação for alto e negativo, isso significaria que um crescimento econômico mais forte está associado a uma taxa de desemprego mais baixa.
- No mundo das finanças, o coeficiente de correlação pode ser usado para analisar a relação entre o retorno de dois investimentos. Um investidor poderia analisar a correlação entre o retorno de um fundo de ações e o retorno de um fundo de títulos.
Se o coeficiente de correlação for baixo ou negativo, isso significaria que os dois investimentos são relativamente independentes, o que poderia ser desejável para um portfólio diversificado.
Benefícios e Limitações do Coeficiente de Correlação de Pearson
O coeficiente de correlação de Pearson oferece diversos benefícios, mas também possui limitações que devem ser consideradas.
- Um dos principais benefícios do coeficiente de correlação é sua capacidade de quantificar a força e a direção da relação linear entre duas variáveis. Isso permite que os pesquisadores compreendam a natureza da relação entre as variáveis e façam previsões mais precisas.
- O coeficiente de correlação também é relativamente fácil de calcular e interpretar, tornando-o uma ferramenta acessível para pesquisadores de diferentes áreas.
- No entanto, o coeficiente de correlação de Pearson possui algumas limitações. Ele só pode medir relações lineares entre variáveis. Se a relação entre as variáveis for não linear, o coeficiente de correlação pode subestimar a força da relação.
- Outra limitação é que o coeficiente de correlação é sensível a valores discrepantes. Um único valor discrepante pode distorcer significativamente o coeficiente de correlação, levando a conclusões imprecisas.
Comparação com Outros Métodos de Análise de Correlação
O coeficiente de correlação de Pearson não é o único método disponível para analisar a relação entre variáveis. Outros métodos, como o coeficiente de correlação de Spearman, também são usados.
- O coeficiente de correlação de Spearman é uma medida de correlação de posto, o que significa que ele mede a relação entre os postos das variáveis, em vez dos valores reais. Isso torna o coeficiente de Spearman menos sensível a valores discrepantes do que o coeficiente de Pearson.
- O coeficiente de correlação de Spearman também pode ser usado para analisar relações não lineares entre variáveis, enquanto o coeficiente de Pearson só pode medir relações lineares.
- No entanto, o coeficiente de Spearman fornece menos informações sobre a força e a direção da relação entre as variáveis do que o coeficiente de Pearson.
Interpretação dos Resultados: Exemplos De Coeficiente De Correlação De Pearson
Agora que você aprendeu a calcular o coeficiente de correlação de Pearson, é hora de entender o que esses números significam! O coeficiente de correlação, que varia de -1 a 1, nos dá uma medida da força e da direção da relação linear entre duas variáveis.
Interpretação do Valor do Coeficiente de Correlação
Um valor de 1 indica uma correlação positiva perfeita, ou seja, as duas variáveis aumentam juntas de forma linear. Um valor de -1 indica uma correlação negativa perfeita, onde as variáveis diminuem juntas de forma linear. Um valor de 0 indica que não há correlação linear entre as variáveis.
Aqui estão alguns exemplos para ilustrar:
- Se o coeficiente de correlação entre o número de horas de estudo e a nota em um teste for 0,8, isso indica uma forte correlação positiva. Isso significa que, à medida que o número de horas de estudo aumenta, a nota no teste tende a aumentar também.
- Se o coeficiente de correlação entre a temperatura ambiente e o número de pessoas usando casacos for -0,7, isso indica uma forte correlação negativa. Isso significa que, à medida que a temperatura ambiente aumenta, o número de pessoas usando casacos tende a diminuir.
- Se o coeficiente de correlação entre a altura de uma pessoa e a sua idade for 0,1, isso indica uma correlação muito fraca. Isso significa que a altura e a idade não estão fortemente relacionadas linearmente.
Gráficos de Dispersão
Gráficos de dispersão são ferramentas visuais muito úteis para entender a relação entre duas variáveis. Eles plotam os pontos de dados para cada variável em um gráfico, permitindo que você visualize a tendência geral.
Aqui estão alguns exemplos de gráficos de dispersão que ilustram diferentes níveis de correlação:
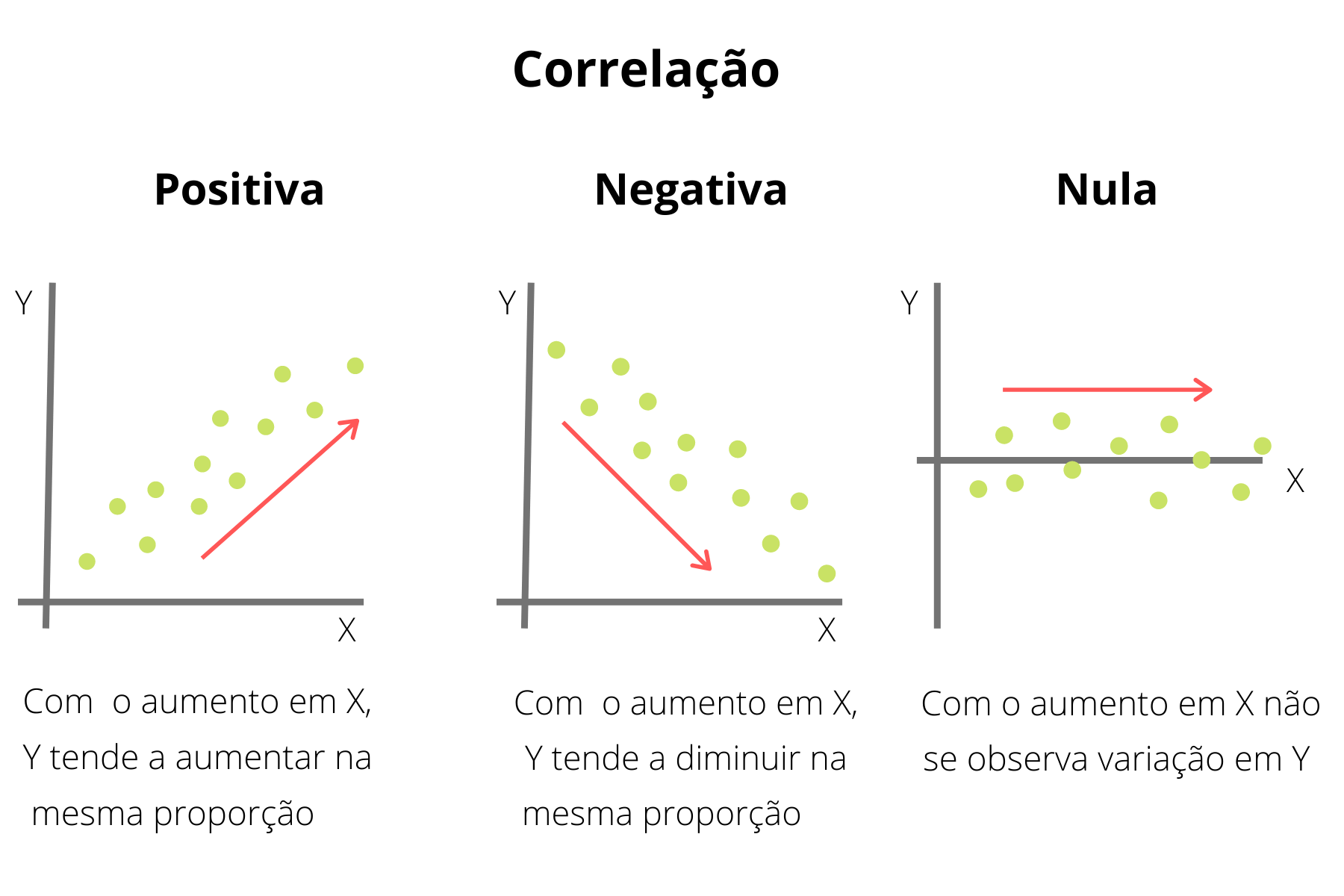
- Correlação Positiva Forte:Os pontos de dados formam uma linha ascendente clara, indicando uma forte relação positiva entre as variáveis.
- Correlação Negativa Forte:Os pontos de dados formam uma linha descendente clara, indicando uma forte relação negativa entre as variáveis.
- Correlação Fraca:Os pontos de dados estão dispersos aleatoriamente, sem uma tendência clara, indicando uma correlação fraca entre as variáveis.
- Sem Correlação:Os pontos de dados estão dispersos aleatoriamente, sem uma tendência clara, indicando que não há correlação entre as variáveis.
Significância Estatística
É importante lembrar que o coeficiente de correlação por si só não é suficiente para concluir que existe uma relação causal entre duas variáveis. A significância estatística do coeficiente de correlação indica a probabilidade de que a relação observada seja devida ao acaso.
Um valor de p baixo (geralmente menor que 0,05) indica que é improvável que a relação observada seja devida ao acaso, sugerindo que existe uma relação real entre as variáveis. Um valor de p alto (geralmente maior que 0,05) indica que é mais provável que a relação observada seja devida ao acaso.
Por exemplo, se o coeficiente de correlação entre o número de horas de estudo e a nota em um teste for 0,8 e o valor de p for 0,01, isso indica que há uma forte correlação positiva entre as variáveis e que é improvável que essa relação seja devida ao acaso.
Considerações Práticas

É fundamental entender as condições e limitações para aplicar o coeficiente de correlação de Pearson de forma eficaz e evitar interpretações errôneas.
Condições Necessárias para Aplicação
O coeficiente de correlação de Pearson é uma ferramenta poderosa para medir a força e direção da relação linear entre duas variáveis. No entanto, é crucial garantir que os dados atendam a certas condições para garantir a validade da análise.
- Dados Contínuos:O coeficiente de correlação de Pearson é mais adequado para variáveis contínuas, que podem assumir qualquer valor dentro de um determinado intervalo. Variáveis discretas, que assumem valores específicos, podem ser analisadas, mas a interpretação dos resultados deve ser feita com cautela.
- Relação Linear:O coeficiente de correlação de Pearson mede a força da relação linear entre duas variáveis. Se a relação não for linear, o coeficiente pode subestimar a verdadeira força da associação. Para verificar se a relação é linear, é recomendável analisar um gráfico de dispersão dos dados.
- Distribuição Normal:O coeficiente de correlação de Pearson assume que os dados de ambas as variáveis seguem uma distribuição normal. Se os dados não forem normalmente distribuídos, o coeficiente pode ser influenciado por valores extremos (outliers).
Lidando com Dados Ausentes e Outliers
Dados ausentes e outliers podem distorcer os resultados da análise de correlação. É importante lidar com esses problemas de forma adequada para garantir a precisão dos resultados.
- Dados Ausentes:Existem várias maneiras de lidar com dados ausentes, como exclusão de casos com valores ausentes, imputação de valores ausentes ou uso de métodos de análise que permitem dados ausentes. A escolha do método depende do tamanho e da natureza dos dados ausentes.
- Outliers:Outliers são valores extremos que podem ter um impacto significativo na correlação. É importante identificar e investigar outliers para determinar se eles são erros de entrada de dados ou valores válidos. Se forem erros, devem ser corrigidos. Se forem valores válidos, é importante considerar o impacto deles na análise e decidir se devem ser removidos ou mantidos.
Cuidados na Interpretação dos Resultados
É importante interpretar os resultados do coeficiente de correlação de forma cuidadosa, considerando as limitações da análise.
- Correlação não implica causalidade:Uma correlação alta entre duas variáveis não significa necessariamente que uma causa a outra. Pode haver uma terceira variável não observada que influencia ambas as variáveis.
- Contexto:É importante considerar o contexto dos dados ao interpretar os resultados. Um coeficiente de correlação alto pode ser significativo em um contexto, mas não em outro.
- Tamanho do efeito:A força da correlação é medida pelo tamanho do coeficiente. Um coeficiente alto indica uma relação forte, enquanto um coeficiente baixo indica uma relação fraca. No entanto, o significado prático do tamanho do efeito depende do contexto específico.
Com o conhecimento do coeficiente de correlação de Pearson, você terá uma nova perspectiva para analisar dados e entender as relações entre diferentes variáveis. Explore os exemplos, pratique os cálculos e lembre-se de considerar as limitações do método para uma análise completa e precisa.
O poder de análise de dados está em suas mãos!

