Planejamento de Aula de Matemática: Ensino Fundamental II: Exemplo De Plano De Aula De Matematica Ensino Fundamental 2
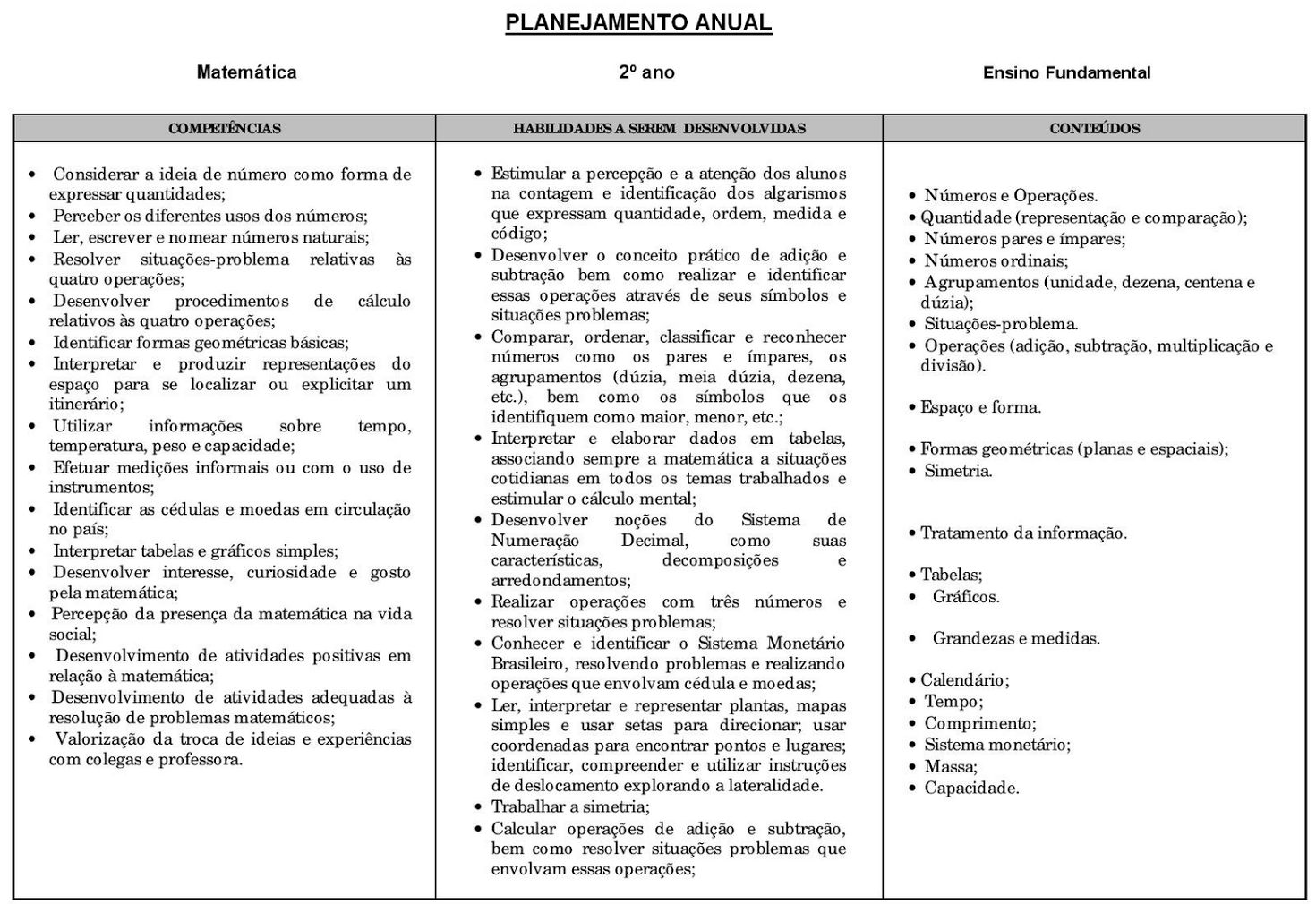
Exemplo De Plano De Aula De Matematica Ensino Fundamental 2 – Um plano de aula bem estruturado é fundamental para o sucesso do ensino de matemática no Ensino Fundamental II. Ele garante a organização do conteúdo, a adequação às necessidades dos alunos e a avaliação eficaz da aprendizagem. A clareza e a sequência lógica das atividades contribuem para uma experiência de aprendizagem mais significativa e duradoura, promovendo o desenvolvimento do raciocínio lógico-matemático e a construção de competências essenciais para a vida.
Objetivos de Aprendizagem: Frações
Os objetivos gerais de aprendizagem para este plano de aula, focado no tema frações, são: compreender o conceito de fração como parte de um todo; representar frações de diferentes maneiras (gráfica, numérica); comparar e ordenar frações; e resolver problemas envolvendo frações no contexto do cotidiano.
Recursos Didáticos
A seleção cuidadosa dos recursos didáticos é crucial para tornar a aula mais engajadora e acessível a todos os alunos. A variedade de materiais permite atender diferentes estilos de aprendizagem e promover a interação com o conteúdo de forma significativa.
| Recurso | Função | Utilização | Justificativa |
|---|---|---|---|
| Material concreto (barras de frações, círculos de frações) | Visualizar e manipular frações, facilitando a compreensão do conceito. | Os alunos irão manipular as barras e círculos para representar e comparar frações. | Permite a aprendizagem concreta e manipulativa, ideal para alunos com dificuldades de abstração. |
| Software educativo (ex: GeoGebra) | Representar frações graficamente e realizar operações com frações de forma dinâmica. | Os alunos usarão o software para visualizar frações, criar representações gráficas e explorar propriedades. | Oferece recursos visuais interativos, motivando os alunos e permitindo a exploração individualizada. |
| Lousa interativa ou quadro branco | Apresentar exemplos, explicações e resolver problemas coletivamente. | O professor utilizará a lousa para explicar conceitos, apresentar exemplos e interagir com os alunos. | Facilita a visualização e a participação ativa de toda a turma. |
| Folhas de atividades impressas | Aplicar os conceitos aprendidos através de exercícios. | Os alunos resolverão exercícios individuais ou em grupo para consolidar o aprendizado. | Permite a avaliação individual do aprendizado e a prática de resolução de problemas. |
Desenvolvimento da Aula: Atividades e Metodologias
As atividades propostas seguem uma sequência lógica, partindo de atividades mais concretas para atividades mais abstratas, visando atender às diferentes etapas de aprendizagem dos alunos. A variedade de atividades estimula a participação e o envolvimento de todos.
- Atividade 1: Manipulação de Materiais Concretos:
- Distribuir barras e círculos de frações para cada aluno.
- Solicitar que representem diferentes frações usando os materiais.
- Comparar frações representadas pelos alunos, promovendo a discussão e a construção coletiva do conhecimento.
- Atividade 2: Uso de Software Educativo:
- Utilizar o GeoGebra para representar frações graficamente.
- Criar representações visuais de frações e realizar operações simples (adição e subtração).
- Explorar as propriedades das frações através de atividades interativas do software.
- Atividade 3: Resolução de Problemas Contextualizados:
- Apresentar problemas do cotidiano que envolvam frações (ex: dividir uma pizza, calcular porcentagens).
- Incentivar os alunos a resolver os problemas individualmente ou em grupo, utilizando os recursos aprendidos.
- Discutir as diferentes estratégias de resolução e os resultados obtidos.
Atividade 1 é ideal para introduzir o conceito de forma concreta, enquanto a Atividade 2 explora a representação gráfica e as operações. A Atividade 3 foca na aplicação prática em contextos reais, consolidando o aprendizado. A sequência permite uma progressão natural do concreto para o abstrato.
Avaliação da Aprendizagem
A avaliação será contínua e abrangente, utilizando diferentes instrumentos para verificar a compreensão dos alunos. A observação da participação, a análise das atividades e a aplicação de uma prova escrita permitem uma avaliação completa e justa do aprendizado.
A avaliação será realizada através da observação da participação nas atividades em grupo, da análise das resoluções dos exercícios individuais e de uma prova escrita com problemas contextualizados. Os resultados serão utilizados para ajustar o plano de aula em aulas futuras, focando em pontos que necessitem de maior atenção.
Exemplo de Atividade Avalitiva: Resolver os seguintes problemas:
- Maria comeu 1/4 de uma pizza e João comeu 2/8. Quem comeu mais pizza?
- Ana tem 1/2 metro de fita. Ela precisa de 3/4 de metro para fazer um laço. Quanto de fita ainda falta?
Critérios de Correção: Correção da resolução dos problemas, demonstrando o entendimento do conceito de frações e a capacidade de resolução de problemas contextualizados.
Adaptação e Diferenciação, Exemplo De Plano De Aula De Matematica Ensino Fundamental 2
Para atender às necessidades de alunos com diferentes estilos de aprendizagem, o plano de aula será adaptado utilizando diferentes recursos e estratégias. Alunos com dificuldades poderão receber apoio extra com atividades mais concretas e simplificadas, enquanto alunos com maior facilidade poderão ser desafiados com atividades de enriquecimento.
Atividades de Reforço: Uso de materiais concretos adicionais, atividades com menor grau de complexidade, exercícios de repetição.
Atividades de Enriquecimento: Problemas mais complexos, pesquisas sobre o tema, atividades que envolvam a criação de jogos com frações.
A inclusão de recursos como jogos, softwares e atividades manipulativas contribui para a aprendizagem de todos os alunos, permitindo que cada um aprenda no seu ritmo e da maneira que melhor se adapta ao seu estilo de aprendizagem.
Ilustrações e Exemplos Práticos
Uma ilustração eficaz para representar o conceito de fração seria um círculo dividido em partes iguais, com algumas partes coloridas para representar a fração. Por exemplo, um círculo dividido em 4 partes iguais, com 3 partes coloridas, representaria a fração 3/4. As cores vibrantes e a divisão clara do círculo contribuiriam para um entendimento visual imediato.
Exemplo numérico: Se uma barra de chocolate tem 12 quadrados e você come 3, você comeu 3/12 da barra, que simplificada é 1/4.
Problema contextualizado: Pedro precisa pintar 2/3 de uma parede. Se a parede tem 9 metros quadrados, quantos metros quadrados Pedro precisa pintar?
Quais são os principais desafios em ensinar matemática no Ensino Fundamental II?
Os principais desafios incluem a diversidade de estilos de aprendizagem, a necessidade de contextualizar o conteúdo, a superação de dificuldades específicas em conceitos matemáticos e a adaptação do ensino a alunos com necessidades educacionais especiais.
Como posso adaptar este plano de aula para diferentes níveis de proficiência matemática?
A adaptação pode ser feita através da diferenciação pedagógica, oferecendo atividades de reforço para alunos com dificuldades e atividades de enriquecimento para alunos com maior facilidade. A complexidade dos problemas e exercícios pode ser ajustada de acordo com o nível de cada aluno.
Que tipo de avaliação formativa pode ser utilizada além das citadas no plano?
Portfólios de trabalhos, autoavaliações, registros de observação da participação em atividades em grupo e debates em sala de aula são exemplos de avaliações formativas complementares.

