Equação Do 2º Grau: Como Resolver (Exemplos E Exercícios) – a frase soa como um desafio, não é? Mas prepare-se para descobrir que desvendar o mistério das equações de segundo grau é uma jornada fascinante, repleta de insights e conquistas. Vamos embarcar juntos nessa aventura matemática, desvendando conceitos fundamentais, dominando métodos de resolução poderosos e aplicando todo esse conhecimento em situações práticas, do mundo da física à elegância da geometria.
Prepare-se para superar obstáculos, celebrar vitórias e, acima de tudo, expandir seus horizontes matemáticos.
Neste guia completo, exploraremos a estrutura da equação do segundo grau, compreendendo seus diferentes tipos e aprendendo a identificá-los com facilidade. Dominaremos a fórmula de Bhaskara, um instrumento poderoso para resolver qualquer equação, e exploraremos o método da fatoração, uma técnica elegante e eficiente para casos específicos. Veremos como interpretar os resultados, entendendo o significado do discriminante e o que ele revela sobre a natureza das raízes.
Através de exemplos práticos e exercícios resolvidos, você estará pronto para enfrentar qualquer desafio que envolva equações de segundo grau.
Conceitos Fundamentais da Equação do 2º Grau

A equação do 2º grau, uma ferramenta matemática de poder inigualável, abre as portas para a resolução de inúmeros problemas em diversas áreas, desde a engenharia à economia. Sua elegância reside na capacidade de modelar situações complexas com uma expressão aparentemente simples, revelando soluções que, muitas vezes, permanecem ocultas à primeira vista. Compreender seus fundamentos é a chave para desvendar seus mistérios e dominar sua aplicação.A forma geral da equação do 2º grau é representada por
ax² + bx + c = 0
, onde ‘a’, ‘b’ e ‘c’ são números reais, sendo ‘a’ diferente de zero. Este detalhe é crucial: a presença do termo quadrático (ax²) define a equação como sendo de segundo grau. ‘a’ é o coeficiente do termo quadrático, ‘b’ o coeficiente do termo linear e ‘c’ o termo constante. Cada um desses coeficientes desempenha um papel fundamental na determinação das características da equação e, consequentemente, de suas raízes – as soluções da equação.
Tipos de Equações do 2º Grau
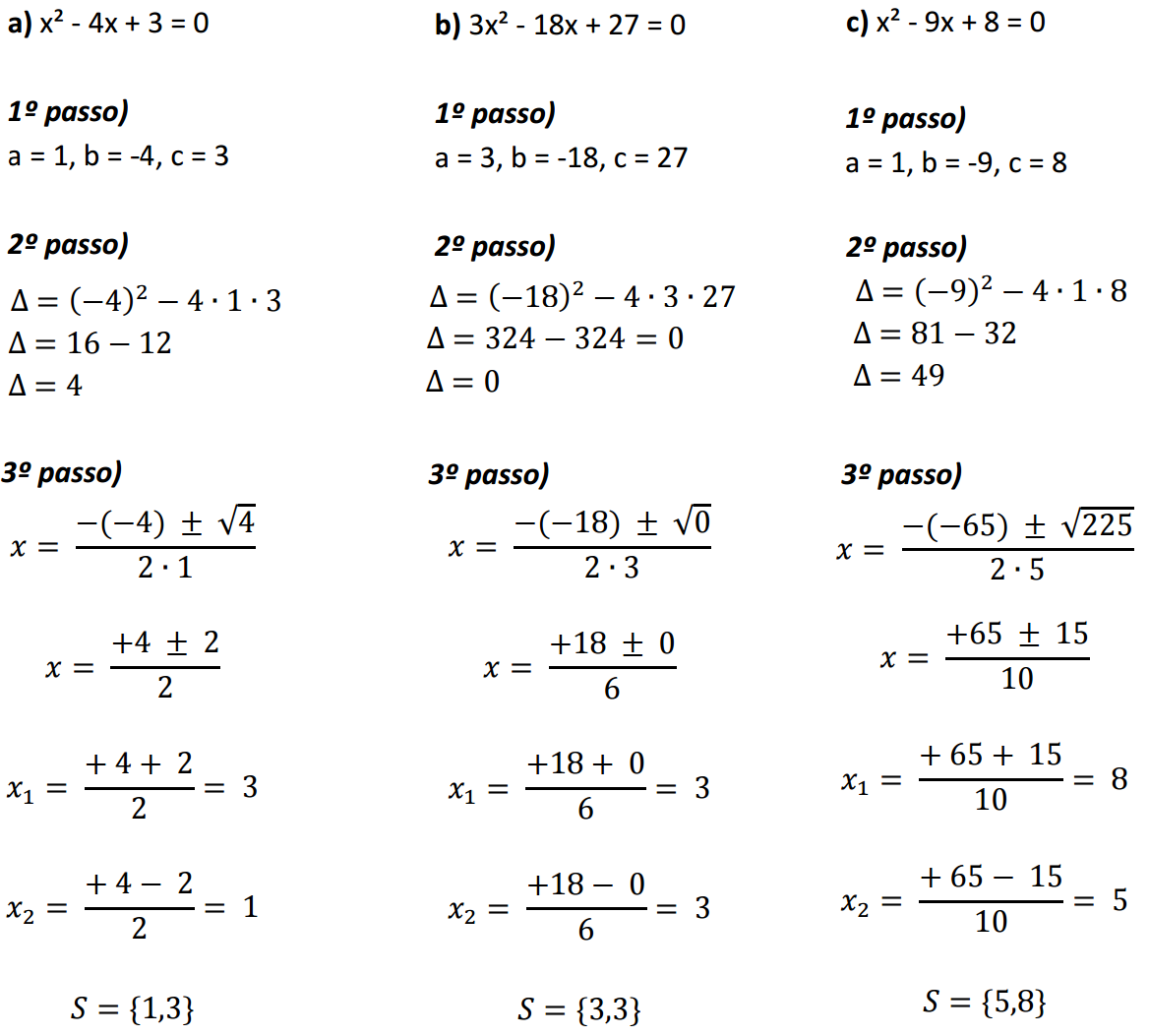
As equações do 2º grau podem ser classificadas em diferentes tipos, dependendo dos valores dos coeficientes ‘a’, ‘b’ e ‘c’. Essa classificação facilita a escolha do método de resolução mais adequado e eficiente.
Comparação dos Tipos de Equações do 2º Grau e seus Métodos de Resolução
A tabela abaixo apresenta uma comparação concisa dos diferentes tipos de equações do 2º grau, seus métodos de resolução e exemplos ilustrativos. A escolha do método mais eficiente depende da forma da equação.
| Tipo de Equação | Forma da Equação | Método de Resolução | Exemplo |
|---|---|---|---|
| Completa | ax² + bx + c = 0 (a ≠ 0, b ≠ 0, c ≠ 0) | Fórmula de Bhaskara ou método de completar quadrados | 2x² + 5x – 3 = 0 |
| Incompleta Pura | ax² + c = 0 (a ≠ 0, b = 0) | Isolamento da variável x | 3x² – 12 = 0 |
| Incompleta Mista | ax² + bx = 0 (a ≠ 0, c = 0) | Fatoração por x | x² – 4x = 0 |
Aplicações e Interpretação de Resultados: Equação Do 2º Grau: Como Resolver (Exemplos E Exercícios)

A equação do 2º grau, embora pareça um conceito abstrato da matemática, é uma ferramenta poderosa com aplicações surpreendentemente vastas no mundo real. Sua elegância reside na capacidade de modelar situações diversas, desde o lançamento de um projétil até o cálculo da área de uma figura geométrica. A interpretação dos resultados, por sua vez, revela segredos ocultos na própria estrutura do problema.
Vamos desvendar esse poder.
A solução de uma equação do 2º grau, representada pelas suas raízes, oferece insights cruciais sobre o problema em questão. A chave para essa interpretação reside no discriminante (Δ), que, como um oráculo matemático, nos revela a natureza dessas raízes.
Interpretação do Discriminante (Δ)
O discriminante (Δ = b²
4ac) é um farol que ilumina o caminho da solução. Seu valor determina a natureza das raízes da equação
se são reais e distintas, reais e iguais, ou imaginárias. Quando Δ > 0, a equação possui duas raízes reais e distintas, significando que o problema modelado apresenta duas soluções possíveis e diferentes. Se Δ = 0, as raízes são reais e iguais, indicando uma única solução para o problema. Finalmente, se Δ < 0, as raízes são complexas (imaginárias), revelando uma ausência de soluções reais no contexto do problema.
Exemplos de Aplicações em Física e Geometria
A equação do 2º grau surge naturalmente em diversos contextos.
Na física, por exemplo, a trajetória de um projétil lançado obliquamente é descrita por uma parábola, cuja equação é do 2º grau. A distância horizontal percorrida pelo projétil antes de tocar o solo pode ser calculada resolvendo uma equação quadrática. Em geometria, o cálculo da área de um retângulo com uma relação específica entre comprimento e largura também leva a uma equação do 2º grau.
Por exemplo, se a área de um retângulo é 12m² e o comprimento é 3m maior que a largura, podemos modelar o problema com a equação x(x+3) = 12, onde x representa a largura. Resolvendo essa equação, encontramos as dimensões do retângulo.
Exemplo com Raízes Imaginárias

Imagine um problema que envolve o cálculo da altura de um objeto lançado verticalmente para cima, considerando apenas a ação da gravidade. A equação que descreve a altura (h) em função do tempo (t) pode ser representada por h(t) = -5t² + 20t +
- Se quisermos determinar o instante em que a altura é de 200 metros, teremos a equação: -5t² + 20t + 100 = 200. Simplificando, obtemos -5t² + 20t – 100 = 0, ou t²
- 4t + 20 = 0. Calculando o discriminante, Δ = (-4)²
-4(1)(20) = -64. Como Δ < 0, as raízes são imaginárias.
Neste caso, as raízes imaginárias indicam que o objeto nunca atingirá a altura de 200 metros. A altura máxima atingida pelo objeto é inferior a 200 metros, sendo determinado pelas raízes da equação que modela a trajetória do objeto.
Exercício Resolvido, Equação Do 2º Grau: Como Resolver (Exemplos E Exercícios)

Um fazendeiro deseja cercar um terreno retangular com 100 metros de cerca. Ele deseja que o terreno tenha uma área de 600 m². Quais são as dimensões do terreno?
Seja x o comprimento e y a largura do terreno. Sabemos que o perímetro é 2x + 2y = 100, e a área é xy =
600. Da primeira equação, temos y = 50 – x. Substituindo na segunda equação, obtemos x(50 – x) =
600. Simplificando, chegamos à equação do 2º grau: x²
-50x + 600 = 0.
Resolvendo esta equação, por exemplo, utilizando a fórmula de Bhaskara, encontramos as raízes x₁ = 20 e x₂ = 30. Portanto, as dimensões do terreno são 20 metros por 30 metros (ou vice-versa).

